Tackling Backtracking Search
Introduction
Anyone who’s taken CPSC 110 at UBC probably experiences a sense of dread when they hear about search problems. This is not an unreasonable response — backtracking search problems are among the hardest that you’ll encounter on interview practice sites like Leetcode, so it seems almost cruel to expect first year computer science students (many of whom have never programmed in their life) to be able to tackle them. However, like with any other problem that you’ll encounter in 110 (or in software engineering generally), having a structured approach to backtracking can help turn a seemingly gargantuan task into one that’s quite digestible. There’s only one way to eat an elephant — one bite at a time.
Premise
The premise of backtracking search problems is to generate an n-ary (or arbitrary-arity) tree of potential solutions to our problem, and then searching through that generated tree to find our solution. As a quick reminder, an n-ary tree is a tree where each node can have an arbitrary number of children. This differs from a binary search tree, where each node has exactly two children.
Illustrative exampe: N-Queens
I’ll be using the N-Queens problem to demonstrate my approach to backtracking search problems:
How can N queens be placed on an NxN chessboard so that no two of them attack each other?
For example, 4 queens can be placed on a 4x4 chess board like this:
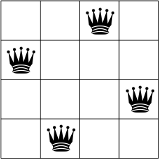
While this may seem intimidating at first, as you’ll see a structured approach will make this problem much easier.
Tools
I’ll be using Go to develop my solution to this problem, but I won’t be using any third-party packages so you should be able to reproduce my solution in your language of choice.
Modelling the search state
The first step in any backtracking search problem is to determine what we are searching for, and how to best represent that in a data structure. This will represent the ’node’ in the tree of solutions we are searching through.
In the context of the N-queens problem, we are looking for a chess board that contains N-queens that cannot attack each other. A chess board is essentially a grid, which can be represented using a 2-dimensional array. We also need a way to represent which squares in the board contain a queen. This can be done using a boolean value — true means a queen is in that square, and false means it’s empty.
A simple function can be used to generate an empty board of size N x N.
// Queen represents position (row, column) of a Queen on a chess board
type Queen [2]int
// Board is a two-dimensional array of boolean values representing a chess board
type Board [][]bool
// NewBoard creates an empty Board of size n x n
func NewBoard(n int) *Board {
board := make(Board, n)
for i := 0; i < n; i++ {
board[i] = make([]int, n)
for j := 0; j < n; j++ {
board[i][j] = false
}
}
return &board
}
Generating child nodes
The empty board we generated in step 1 will be our starting point – the root node of our search space. To generate candidate child nodes, fill each empty square with a queen and then verify if the board that we’ve produced is valid. If we start with an empty 2 x 2 board, as our root, there are four valid child nodes that we can produce:
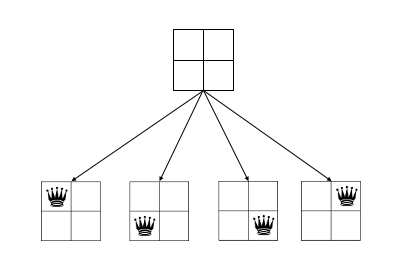
Once we’ve generated the child nodes and eliminated any invalid boards, we will visit each one of them in turn and check if any of them represent a solved board – i.e. a board with N queens. Since any invalid boards have already been eliminated from the tree, if we encounter a board with N queens it’s guaranteed to be a valid solution. This process can be repeated recursively until either a solution is found, or no valid child nodes can be generated. In our 2 x 2 example above, there is no valid arrangement of 2 queens such that they cannot attack each other, so the search would fail.
// nextBoards takes an existing board and creates a slice of new boards
// with each empty space filled with a queen.
// E.g.
// F F T F F T F F F F
// F F -> F F, F F, T F, F T
func (b *Board) nextBoards() []*Board {
n := len(*b)
boards := make([]*Board, 0)
// Loop through b, fill every empty slot with a queen
for i := 0; i < n; i++ {
for j := 0; j < n; j++ {
// Check if slot already has a queen
if (*b)[i][j] {
continue
}
// Create a new board
newBoard := b.duplicate()
// Fill slot with a new queen
newBoard[i][j] = true
// Add board to list of boards if it is valid
if newBoard.valid() {
boards = append(boards, &newBoard)
}
}
}
return boards
}
Validating boards
Before adding newly generated boards to the search space, we need to make sure that they’re valid. This effectively means looping through each queen in the board and making sure that it doesn’t attack any other queen on the board. We can eliminate queens with the same row or column index easily, and we can check diagonals by checking the absolute value of the difference in row and column indices. If both the row and column deltas are the same, the two queens are on a diagonal.
// valid returns true if all queens in the board cannot attack any other queen
func (b *Board) valid() bool {
n := len(*b)
// Find indices of all queens in the board
queens := make([]Queen, 0)
for i := 0; i < n; i++ {
for j := 0; j < n; j++ {
if (*b)[i][j] {
queens = append(queens, Queen{i, j})
}
}
}
for i, queen := range queens {
if len(queens[i:]) == 0 {
break
}
if queen.attacks(queens[i+1:]) {
return false
}
}
return true
}
// attacks checks if q attacks any of the queens
func (q Queen) attacks(queens []Queen) bool {
for _, queen := range queens {
if q[0] == queen[0] || q[1] == queen[1] || q.diagonal(queen) {
return true
}
}
return false
}
// diagonal returns true if q and queen are on a shared diagonal
func (q Queen) diagonal(queen Queen) bool {
dx := int(math.Abs(float64(q[1] - queen[1])))
dy := int(math.Abs(float64(q[0] - queen[0])))
return dx == dy
}
Put it all together
Now that we know how to generate child nodes and check if they’re valid, the last thing to do is put it all together into a search function.
At a high level, this function consumes a board and will do the following:
- Check the board to see if it’s solved. If it is, return it. If not, proceed to step 2.
- Generate child nodes
- Recursively search each child node one by one, returning the result if a solution is found
- If a solution cannot be found, return an error
func search(board *Board) *Board, err {
if board.solved() {
return board
}
nextBoards := board.nextBoards()
for board := range nextBoards {
solution, err := search(board)
if err != nil {
continue
}
return solution
}
return nil, fmt.Errorf("unable to find a solution")
}
Conclusion
Hopefully this post has helped you develop some intuition around search problems and given you a framework for approaching them in the future. You can check out a working implementation of the N-Queens solver we developed from my Github if you want to see it in action. I would encourage you to try to solve this problem from scratch without referencing any of my code to ensure that you’ve really grasped the concepts. If you’re interested in checking out some other search problems, Peter Norvig has an excellent tutorial on building a Sudoku solver. If you have any suggestions for how to make this post better, feel free to reach out to me via email or Twitter. Happy searching!
